mathsHeuristics Centre Holiday Break

The centre will be closed from 13th Dec 2010 to 3rd Jan 2011 for our annual short break. Do email us at enquiry@mathsheuristics.com and we will get back to you a.s.a.p. Thank you for the wonderful 2010 and have a great holiday!

ST Forum: Why all that drilling may not count for much

Why all that drilling may not count for much

I REFER to the letter by Mr Wong Tuck Yin on Tuesday ("Express stream entry rate"). He said that despite the extensive exam preparations, the 63.5 per cent rate for Express stream entry was low and therefore it must be because the Primary School Leaving Examination (PSLE) was too difficult.
He failed to consider the possibility that the preparation method was flawed. Intensive worksheet practice only helps students to be exposed to different types of exam questions, but it does not teach them how to tackle a question that they have never encountered before.
Based on our study of exam performance of Primary 6 pupils for science and maths, study skills, conceptual understanding and question practice are heavily emphasised in the preparation for exams. Yet one very essential skill set is usually left out - a thinking framework for answering exam questions. Pupils need a thinking framework to approach questions in a systematic manner that will lead them to the right answer expressed correctly on paper. Without such a framework, practice does not necessarily make perfect.
When pupils are explicitly taught a thinking framework to tackle maths and science questions, they experience a marked improvement in their ability to answer different types of questions without the need for drilling. It's no surprise that their grades also improve dramatically.
It is time for parents to stop and think of a different way to prepare their children for PSLE.
Sunny Tan
Principle Trainer, Author
Maths Heuristics Pte Ltd

Source: http://www.straitstimes.com/STForum/OnlineStory/STIStory_610167.html 

Sunny Tan's Interview by 93.8 LIVE!

The better way to study for exams

Exams are important, but according to expert educator, Sunny Tan, parents have it wrong when it comes to helping their children prepare.

There's just too much worksheet drilling, especially in tuition centres when it comes to exams such as PSLE.

He has devised a novel approach known as the Unit Transfer Method that simplifies the learning of math.

Learn more here

Listen to [ 1 ] | [ 2 ]

The Straits Times - Heuristics: The ladder to A*/A in PSLE Maths and Science

Heuristics

Parents Preview @ SMU

Click on the image for a larger version

Expert Opinions - Singapore's Child (Oct 2010)

Sunny Tan, mathsheuristics innovator shares his insights with Singapore's Child magazine - Exam Tips on the run

Unit Transfer Method Book Sold Out!

The Unit Transfer Method has sold over a thousand copy and it is currently out of stock. Thank you one and all for your support.

Mastering Heuristics Series Authors Exclusive Interview in TODAY

"Mastering Heuristics Series Authors Exclusive Interview in TODAY"

TODAY speaks to Sunny Tan, author of the Mastering Heuristics Series and Principle Trainer at mathsHeuristics™, and discovers firsthand how Unit Transfer Method (UTM) helps children and parents solve challenging Maths problems with ease.

(Click on the Picture below to view pdf version)

PSLE Higher Order Thinking Skills (for high achievers)

PSLE Maths Explained!

Heuristics of the Week

Every week, we will post a Maths question with step-by-step easy to follow animation, guiding you and your child through the problem-solving process using heuristics approach. You are welcome to contribute questions to the blog by emailing us at utm@mathsheuristics.com. We will post the answers on this blog as soon as time permits.

Featured heuristics: Stack Model

Conventional Model vs Stack Model, Excerpt from Model Approach to Problem Solving

Conventional Model

vs

Stack Model

Excerpt from Unit Transfer Method In Solving Challenging Upper Primary Maths Problems

(Before and After concept: Single unchanged quantities)

Coming Soon....

Readers of the UTM book will soon be able to access to our exclusive easy to follow step-by-step interactive flash explanation online.

UTM- Before and After Concept

Dear Mr Sunny Tan,

May I enquire if unit transfer method can be applied to solve the following problem. If yes, please show me.
Tan X, Y and Z each contained some water. Tank X contains 3 times as much water as Tank Y. After 15% of the water in Tank X and 15% of Tank Y was poured in Tank Z, Tank Z had 30% more than before. If Tank Z had 104 litres of water, how many litres of water had Tank X at first ?

Thank you

Yours sincerely,

Danielle Teo
(your student)

From the Desk of Sunny Tan........  

Case1 - Case 2 (work backwards)

C1 C2-workbacks

Case 1 - Case 2 (Total unchanged quantities)

Case 1 - Case 2

Maths Heuristics featured in Absolutely Parents PSLE Guide 2010

Alternate Approach in solving Challenging Mathematical Problems


Unit Transfer Method offers a simple, logical and yet systematic way for understanding and solving higher-order thinking questions.

Solving mathematical questions using the heuristic of model method requires students to conceptualize a visual model in their mind before translating it onto their worksheet. However, interestingly, not all students are apt in this skill of visualizing. For many such students, UTM appeals more since it uses the prevalent knowledge of ratio and tabulation in analyzing problems. More importantly, complementing UTM with model method, allows students to solve questions in nearly all topics ranging from whole number, fraction, decimal, percentage up to ratio. ... Click Here to continue reading

UTM Question on Repeated Identity

Dear Mr Sunny Tan

I have bought your UTM handbk but unable to solve this question. Hope you will help. 

Andy, Betty, Candy and Danny each has some money. The amount of money Andy has is 1/3 of the total amount of money Betty, Candy and Danny have. The amount of money Betty has is 1/4 of the total amount of money Andy, Candy and Danny have. The amount of money Candy has is 1/5 of the total amount of money Andy, Betty and Danny have. If Danny has $1725, how much do they have altogether?

Mr Teo

From the Desk of Sunny Tan........ 

Pei Hwa Pri/ P6 / 2009 SA1

Alan, Ben, Calvin and Dean shared some postcards. Alan received 20% of the postcards. Ben received 16 fewer postcards than Alan. Calvin received twice as many postcards as Ben. Dean got the remaining 144 postcards.

(a) find the total number of postcards shared by Alan, Ben, Calvin and Dean
(b) how many per cent more postcards than Alan did Dean receive?

Maths Heuristics featured in Kaisu Parent's website

We all know that times have changed, but who would have imagined that the foundational mathematical problem solving skills we were brought up on mean practically nothing for our next generation?

The mathematics questions found in primary schools these days can leave even the most academically inclined parents stumped! Regardless whether you’ve scored A* in your own PSLE maths paper decades ago, we’re sure you’ve had difficulty trying to guide your child with his/her homework using your old-school algebraic equations. Even the relatively newer model approach, involving drawing rectangular boxes/blocks, doesn’t always work.

Perhaps the alternative Heuristics approach will put those seemingly impossible-to-solve problem sums in a “less intimidating” light. Heuristics simply refers to rules, processes or methods that the student can discover... Click Here to continue reading

Using Equal Concept (UTM) to solve problem!

Utilising Advancd UTM Techniques

Mrs Lim said...

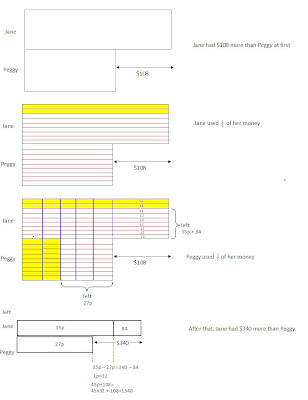
I have bought your Unit Transfer Method Book last month. I was trying to use Chapter 1.4 (All Changing Quanties) to solve the below question from my girl's P6 test paper but somehow just could not solve the question. Question: Jane had $108 more than Peggy at first. Jane used 2/9 of her money while Peggy used 2/5 of her money. After that, Jane had $340 more than Peggy. How many did Jane have at first?

April 11, 2010 9:16 AM

From the Desk of Sunny Tan........

Problems that involve “more than/less than” generally utilize Advanced UTM technique. This problem cannot be solved using “All changing quantities” – questions in “All changing” does not involve “more than/ less than”.

Advance technique involves modification of the basic UTM as follows:

I would advise to teach the child the basic UTM technique and ensure the child is proficient in applying the fundamental UTM framework before to expose them to the advanced UTM. Without the basic training in the UTM framework, the child will faces challenges in visualizing the above conversion and may end up confusing the child.

Below depicts an alternate method to the above problem using the stack model approach :

The Maths Challenge to Parent - UTM book Q5 Pg 20

Hi Sunny

My daughter was trying out the Q5 on page 20 of your UTM book. I have download the answers and explanation, but I don't seem to understand what the "40" in the boxes that you have placed in the diagram. How did you derive the "40"?

Question: Three sisters, Angie, Bernice and Candice share some sweets. Angie's share is 40% of the total number of sweets the three sisters have. Bernice has 40 sweets more than Angie. Bernice's share is 4 times Candice’s. How much money did each of them have?

Thanks

Vijay

From the Desk of Sunny Tan........

The explanation in the book use conventional model. I will illustrate visualizing the model in another perspective - stack model:

Conventional Model VS Stack Model

In my seminars, the following are the most common questions raised by many parents;

a) What are the differences between conventional and stack Model approach?
b) Which model is the more “superior” approach?
c) Will it be confusing for the child to “switch” from conventional to stack model?

Many parents have the misconception that stack Model is completely new approach, that is different from the conventional model. I would like to emphasis that Stack model and conventional Model uses the same fundamental concepts of units to solve problem. Basically, they are the same. The only MAIN difference is the orientation of drawing the model.

Stack model utilizes visual processing technique – enable the child to minimize the movement (rearrange) the models and to combine all the steps required in the conventional model into a single step by using a single model. Then objective is to enable the child to “see” the problems laterally!

I will use the below example to illustrate my point:

The total cost of 14 bags is equal to the total cost of 6 wallets. Each wallet costs $22 more than each bag. Find the cost of each wallet.

CONVENTIONAL MODEL:















STACK MODEL:

Stack Model in action

Conventional Model

Stack Model

Mastering Heuristics Series II

Releasing Soon

Model Approach to Problem-solving
Highly-visual, helps your child to see Maths – literally!

The ability to visualise a problem goes a long way to solving it. The Model Approach to Problem-solving was borne out of this fact. Use drawings (models) in visualising a problem. Go beyond conventional models and solve challenging problems fast with highly-efficient techniques like Stack Model and Split Model.

by Sunny Tan
Releasing in June…

Maths Problem

Hi Sunny,

Greetings!

My daughter, have attended your PR. 6 sesson.

I have one of her Pr. 6 problem that I know the answer but do not know how to present to her. Based on your method, how do you solve the following question:

Ai Tong School organized a 2-day camp. On the first day, the number of boys was 600 more than the girls. On the second day, the number of boys decreased by 10% but the number of girls increased by 10%. If there were 2540 children on the second day, how many children were there on the first day?

Appreciate your enlightening on the solution.

Thanks.

Mr Lee

From the Desk of Sunny Tan........

(click on image for larger view)

Problems Involving Two Variables Concept

Dear Sunny,

I have encountered a math's problem for primary 6, could you please advise me how to solve it?

There were a total of 820 boys and girls at a funfair. After 3/4 of the boys and 3/5 of the girls left the funfair, there were 120 more girls than boys remaining behind. How many boys were there at the funfair at first?

Thanks for your help

Yani

From the Desk of Sunny Tan........